Понятие о вакууме и давлении
Свойства газов при низких давлениях изучаются в физике вакуума, являющейся разделом молекулярно-кинетической теории газов. Основой физики вакуума являются следующие постулаты: 1) газ состоит из отдельных движущихся молекул; 2) существует постоянное распределение молекул газа по скоростям, т. е. одной и той же скоростью обладает всегда одинаковое число молекул; 3) при движении молекул газа нет преимущественных направлений, т. е. пространство газовых молекул изотропно; 4) температура газа — величина, пропорциональная средней кинетической энергии его молекул; 5) при взаимодействии с поверхностью твердого тела молекула газа адсорбируется.
Состояние газа, при котором его давление ниже атмосферного, называется вакуумом. При давлениях, близких к атмосферному, пользуются количественным определением вакуума как разности атмосферного и абсолютного давлений. При абсолютном давлении, отличающемся от атмосферного более чем на два порядка, эта разность остается практически постоянной и не может служить количественной характеристикой разреженного газа. В этих условиях вакуум количественно определяют абсолютным давлением газа. При очень малых давлениях, которые непосредственно уже не могут быть измерены существующими приборами, состояние газа можно характеризовать количеством молекул в единице объема, т. е. молекулярной концентрацией газа.
При взаимодействии молекул газа с поверхностью твердого тела нормальная составляющая изменения количества движения молекулы равна mv cos @; где @ — угол между нормалью к поверхности и вектором скорости; т и v — масса и скорость молекулы. Рассмотрим случай, когда между поверхностью и газовой средой существует энергетическое и адсорбционное равновесие. Каждой адсорбированной молекуле при этом соответствует одна десорбированная молекула с противоположным направлением вектора скорости. Таким образом, суммарное изменение количества движения адсорбированной и десорбированной молекул АК= = 2mv cos @.
Согласно второму закону Ньютона, давление молекулы на поверхность твердого тела
Телесный угол
где г — расстояние между поверхностью и выделенным объемом (рис. 1.1).
Для объема dV в полярной системе координат справедливо выражение
Согласно принятым постулатам, существует распределение молекул по скоростям, поэтому в (1.6) вместо постоянной введем
2 f JL 2 среднеквадратичную скорость молекул -икв=—V т>л Тогда
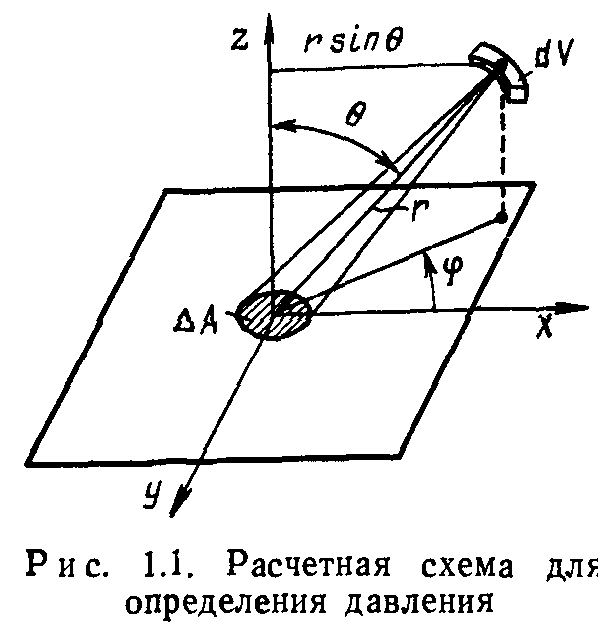


Число молекул в элементарном объеме dV, движущихся в направлении ДЛ, с учетом постулата об отсутствии преимущественных направлений пропорционально телесному углу dco, под которым из центра d/ видна площадка ДЛ

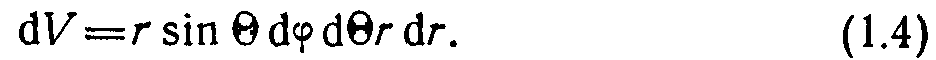

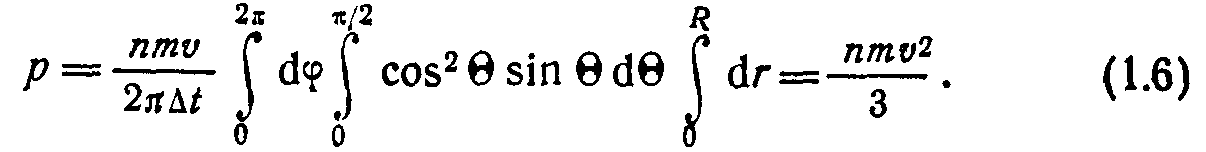
Давление газа на поверхность твердого тела найдем интегрированием по объему полусферы, из которой молекулы достигают поверхности за время Д/, с радиусом R=v&t.
С учетом выражения (1.1)
Подставляя (1.2), (1.3), (1.4) в (1.5), получим
Учитывая, что плотность газа р = пт, выражение (1.7) можно переписать как р=ри2кв/3.
Условия равновесия, использованные при выводе уравнения (1.7), могут не выполняться. Примером является конденсирующая поверхность, с которой из-за очень большого времени адсорбции не происходит десорбции молекул газа. Тело, вылетевшее в космическое пространство из земной атмосферы, десорбирует с поверхности молекулы газа. Количеством же молекул, ударяющихся о поверхность этого тела, можно пренебречь. Для точного расчета давления газа на поверхности твердого тела нужно знать соотношение потоков падающих и вылетающих молекул газа.


