Распределение молекул газа по скоростям
При соударениях друг с другом или со стенками вакуумной камеры молекулы газа изменяют свои скорости как по величине, так и по направлению. Пользуясь гипотезами о существовании стационарного распределения молекул по скоростям и об изотропности пространства газовых молекул, а также учитывая, что. согласно (1.11), среднеквадратичная скорость кв=фЛЗй7’/7тг, Максвелл получил функцию распределения молекул по скоростям
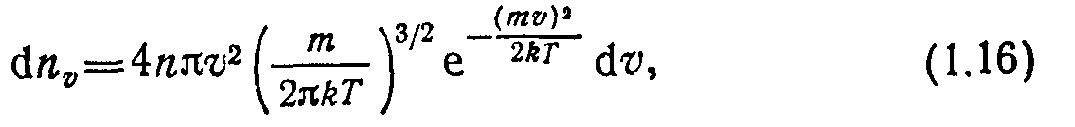
где dnv — число молекул, скорости которых заключены в пределах от v до o + du.
Скорость, при которой наблюдается максимум функции распределения, называется наиболее вероятной скоростью:
Безразмерные функции.

Соотношение между скоростями цвер, flap и икв равно 1:1,128: 1,225. Так, указанные скорости для молекул азота при 0°С составляют пВер=402 м/с, оар=453 м/с, икв==492 м/с. Среднеарифметические скорости молекул некоторых газов при различных температурах приведены в табл. 1.2.
Согласно (1.14), для воздуха при Т=300 К и Л4=29 кг/кмоль при атмосферном давлении поток газовых молекул JVQ=2,9X ХЮ23 см~2-с-1, а из (1.15) объем молекул, ударяющихся о единицу поверхности в единицу времени, VQ=ll,6-10-3 м3/(с-см2).
Преобразуя (1.16), получим функцию распределения молекул по энергиям:
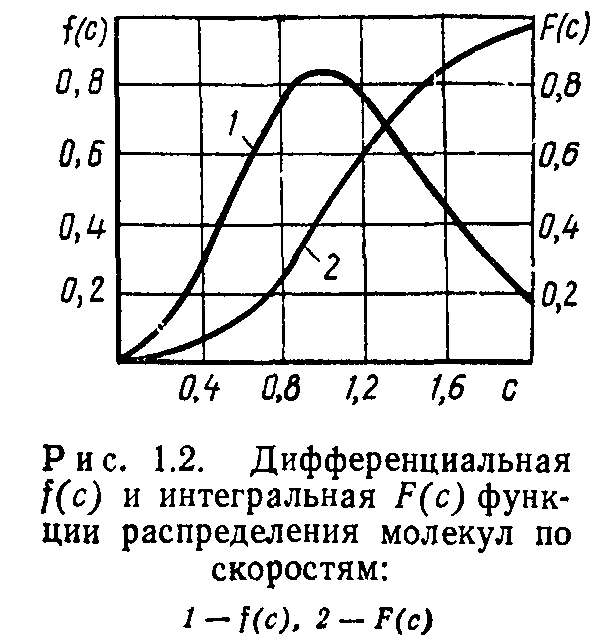
Если ввести обозначение с=ц/оВер, то формулу (1.16) можно переписать так:
представлены на рис. 1.2. Функция F(c) численно равна доле общего числа молекул, скорости которых не превышают с.
В вакуумных расчетах часто используют скорости:
среднеарифметическую

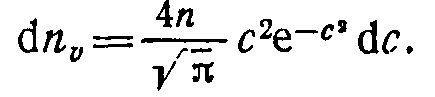

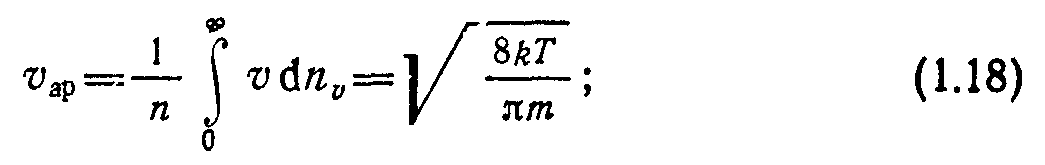

Здесь £, = muKB2/2 — энергия поступательного движения молекулы; dnE— число молекул, энергия которых лежит в интервале от Е до E+dE. Вводя переменную x=E)(kT), получим
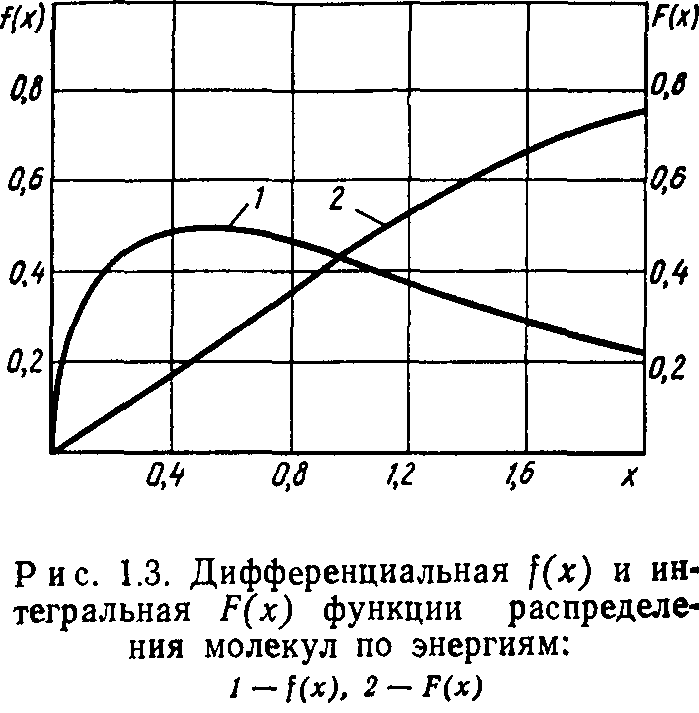

Интегральная кривая, представляющая собой долю молекул" газа, энергия которых меньше Е, определяется функцией
Таблица 1.2
Среднеарифметические скорости молекул некоторых газов при различных температурах
|
Газы |
"ар- “/с |
Газы |
"ар- “/С |
||||||
|
4,2 К |
77 К |
293 К |
600 к |
4,2 К |
77 к |
293 к |
600 к |
||
|
n2 |
56 |
245 |
470 |
672 |
Хе |
26 |
НО |
220 |
311 |
|
Аг |
47 |
200 |
395 |
563 |
Н2О |
70 |
300 |
590 |
839 |
|
о2 |
53 |
225 |
440 |
629 |
Воздух |
54 |
235 |
460 |
661 |
|
СО2 |
45 |
195 |
375 |
536 |
Со |
56 |
245 |
470 |
672 |
|
Ne |
67 |
285 |
555 |
792 |
Не |
150 |
640 |
1250 |
1785 |
|
Кг н2 |
33 210 |
140 906 |
270 1770 |
325 2524 |
сн4 |
75 |
320 |
625 |
889 |
На рис. 1.3 в безразмерной форме представлены графики функций (1.20) и (1.21). Максимум дифференциальной кривой соответствует наиболее вероятной энергии Евер=0,5 kT. Расчет среднеарифметического значения энергии молекул дает Еар — = 1,5 kT.
Наиболее важные значения безразмерных функций даны в табл. 1.3.
Рассмотрим вывод функции распределения (1.16), существование которой постулируется молекулярно-кинетической теорией. Число молекул dn®x, скорости которых заключены в промежутке от vx до Vx+dt»*, пропорционально общему числу молекул п, приращению скорости dvx и определяется функцией

Значения безразмерных функций законов распределения
|
С |
1(c) |
F(c) |
V * |
f(x) |
F(x) |
|
0,1 |
0,0223 |
0,0008 |
0,05 |
0,2401 |
0,0082 |
|
0,2 |
0,0867 |
0,0059 |
0,1 |
0,3229 |
0,0224 |
|
0,3 |
0,1856 |
0,0193 |
0,2 |
0,4131 |
0,0598 |
|
0,4 |
0,3077 |
0,0438 |
0,3 |
0,4578 |
0,1036 |
|
0,5 |
0,4393 |
0,0812 |
0,4 |
0,4785 |
0,1505 |
|
0,6 |
0,5668 |
0,1316 |
0,5 |
0,4839 |
0,1987 |
|
0,7 |
0,6775 |
0,1939 |
0,6 |
0,4797 |
0,2470 |
|
0,8 |
0,7613 |
0,2663 |
0,7 |
0,4688 |
0,2945 |
|
0,9 |
0,8129 |
0,3453 |
0,8 |
0,4535 |
0,3406 |
|
1,0 |
0,8302 |
0,4276 |
0,9 |
0,4352 |
0,3851 |
|
1,2 |
0,7697 |
0,5896 |
1,0 |
0,4152 |
0,4276 |
|
1,4 |
0,6232 |
0,7286 |
1,4 |
0,3294 |
0,5765 |
|
1,6 |
0,4464 |
0,8369 |
1,8 |
0,2502 |
0,6920 |
|
1,8 |
0,2862 |
0,9096 |
2,0 |
0,2160 |
0,7385 |
|
2,0 |
0,1652 |
0,9540 |
3,0 |
0,0973 |
0,8884 |
|
2,5 |
0,0272 |
0,9941 |
5,0 |
0,0170 |
0,9814 |
распределения f(vx). Аналогичные соотношения можно записать для осей координат у и 2. Таким образом,

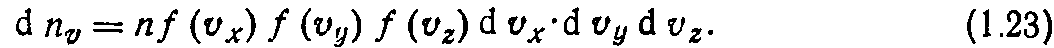

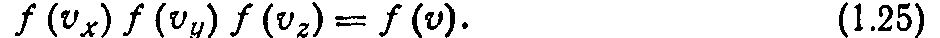

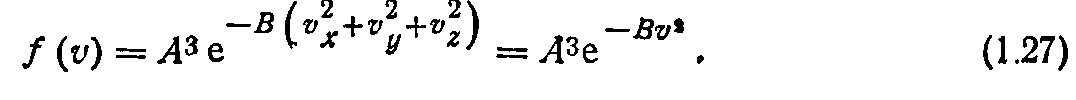
что можно проверить подстановкой (1.26) в (1.25):
Этому уравнению удовлетворяют функции
Функция распределения не зависит от направления и определяется только модулем скорости v, т. е.
Так как пространство газовых молекул изотропно, а концентрация частиц, имеющих скорость v, одинакова во всем пространстве скоростей, то
Число молекул, обладающих скоростями, вектор которых находится внутри параллелепипеда со сторонами dvx, dvy, dnz с учетом независимости координат определяется на основании теории вероятности по формуле
Таким образом, (1.22) с учетом (1.26) можно представить в виде
Уравнение (1.32) устанавливает связь между искомыми постоянными. Для определения их значений воспользуемся выражением для среднеквадратичной скорости из (1.11)

Подставляя (1.29) в (1.33), будем иметь
Значение интеграла в (1.34) найдем согласно (1.31):
тогда, учитывая (1.32) и (1.34), получим
Воспользуемся значениями коэффициентов А и В и перепишем функцию распределения (1.27) в виде
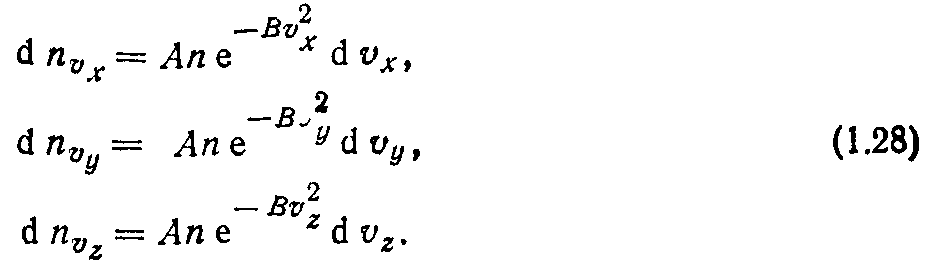

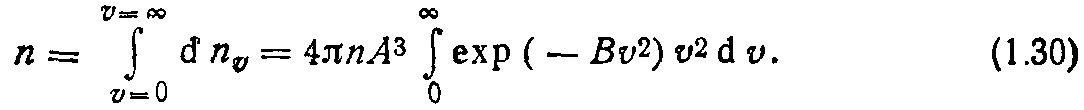


Перепишем выражение (1.23), используя (1.24), (1.25), (1.27):
Для нахождения постоянных А и В проинтегрируем (1.29) по скоростям. Получим
Известно, что
Вычислив интеграл в (1.30) согласно (1.31), имеем

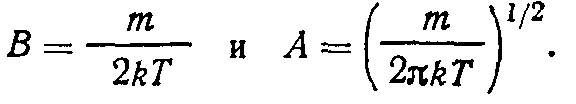

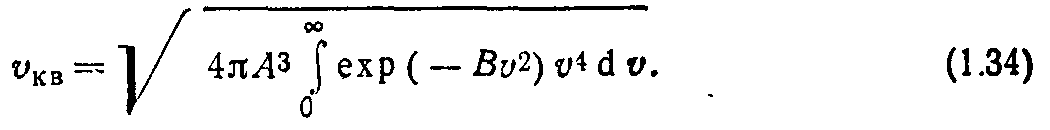

откуда
Тогда число молекул, имеющих скорости в интервале от v до v+dv, согласно (1.29), будет
что совпадает с (1.16).


