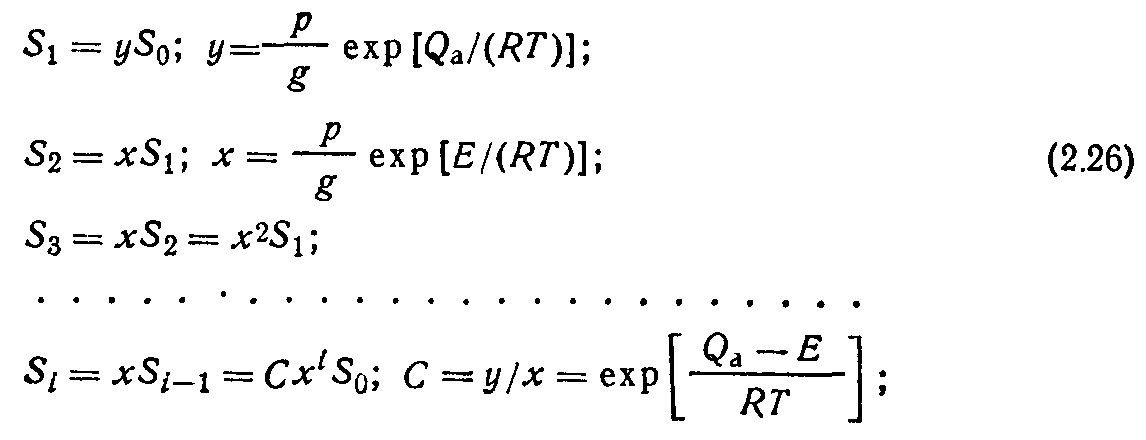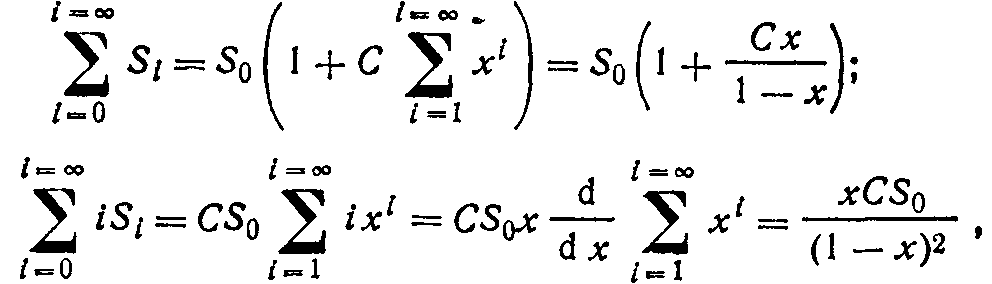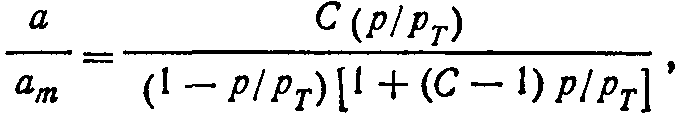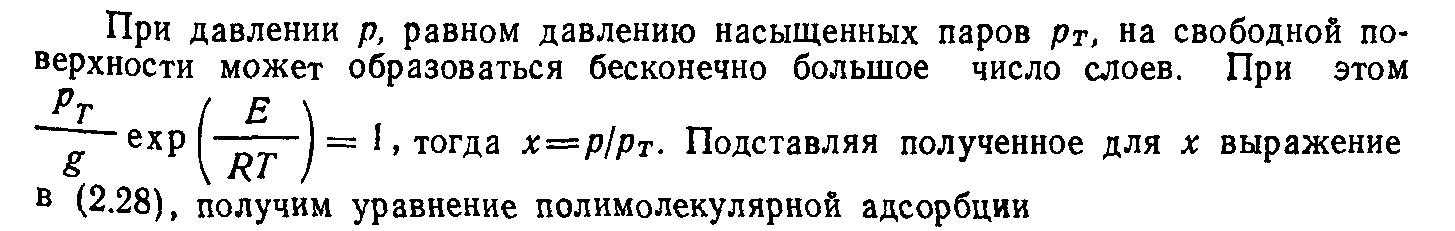изотерма a = F(p) при 7’=const, изобара a = F(T) при p=const и изостера p=F(t) при a=const. Чаще всего пользуются изотермами адсорбции, которые легче всего получить или проверить экспериментальным путем.

Для вывода уравнения изотермы многослойной, полимолекуляр-ной адсорбции сделаем следующие допущения: 1) теплота адсорбции в первом слое постоянная и не зависит от количества поглощенного газа; 2) теплота адсорбции во втором и всех последую-щйх слоях равна теплоте конденсации; 3) значение вероятности конденсации и минимальное время адсорбции одинаковы для всех адсорбционных слоев.

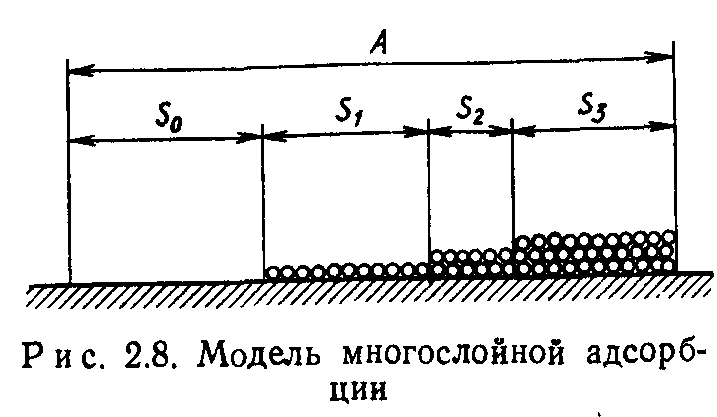
На рис. 2.8 показана условная модель многослойной адсорбции. Молекулы адсорбированы на поверхности в несколько слоев.

Для облегчения расчета свободной поверхности все молекулы условно сдвинуты вправо.

Уравнение полимолекулярной адсорбции было получено Бру-науэром, Эмметом и Тейлором и известно под названием уравнения БЭТ:

Теплоты адсорбции и конденсации некоторых газов приведены в табл. 2.2.

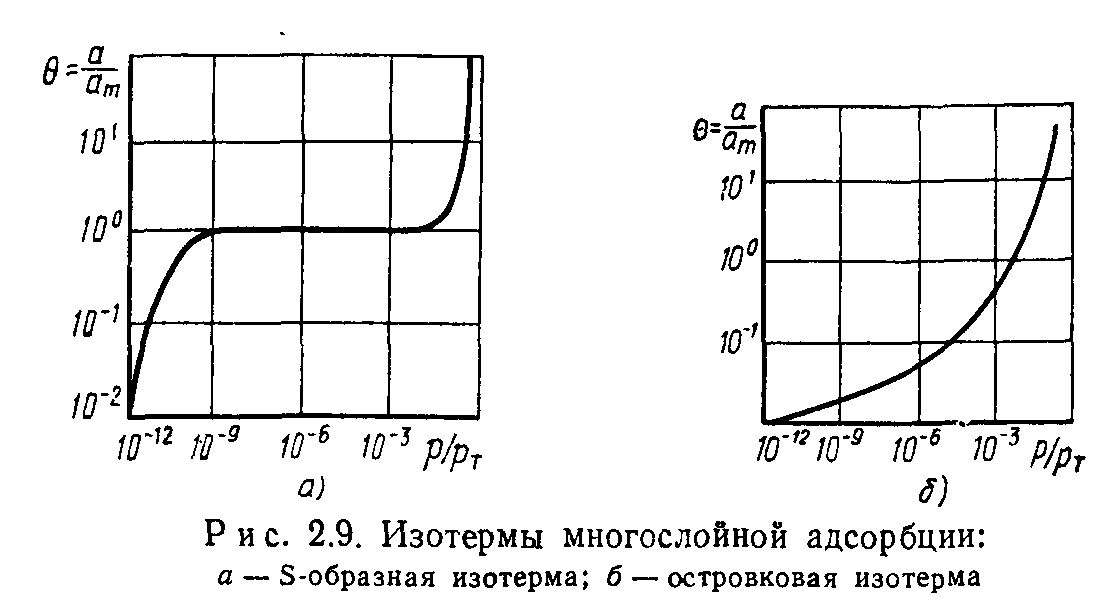
Уравнение (2.17) при Q_a>£ дает S-образную изотерму адсорбции (рис. 2.9, а), а при Q_a^E — островковую изотерму адсорбции (рис. 2.9, б). При островковой изотерме адсорбции поглощение молекул газа на занятой поверхности более вероятно,

чем на свободной. Это приводит к образованию на поверхности многослойных участков поглощенного газа.

Для очень низких давлений р<^рт/С S-образная изотерма переходит в линейную (рис. 2.10, а) и описывается уравнением Генри

где b — постоянная, зависящая от температуры; Ь — С/рт.

Для низких давлений р<£рт S-образная изотерма дает изотерму мономолекулярной адсорбции (рис. 2.10, б)

Уравнение (2.19) известно под названием уравнения Ленгмюра и характерно для хемосорбционных процессов.

На рис. 2.11 показана изотерма (Г=293 К) паров вакуумного масла, имеющего Q_a = 96- 10^е Дж/кмоль, Е’=96-10⁶ Дж/кмоль и

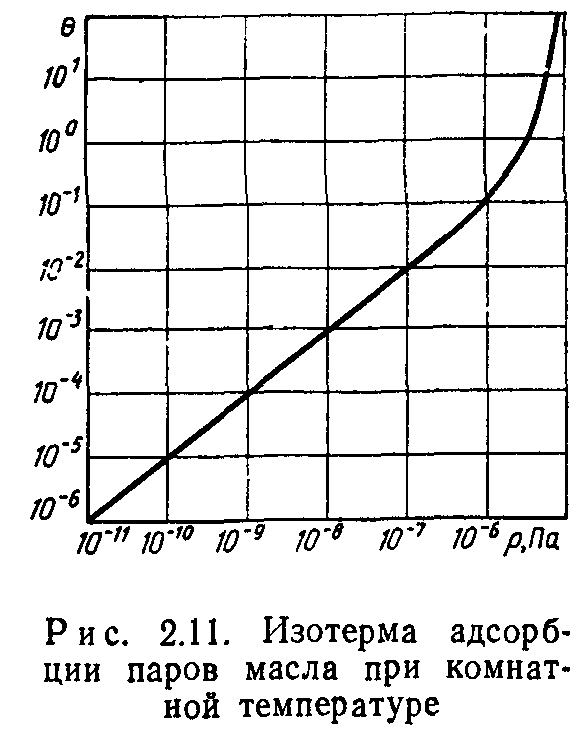
давление насыщенного пара при комнатной температуре Рт= = 10“⁵ Па. Изотерма рассчитана по уравнению (2.17).

Уравнение (2.17) при a=G/A можно преобразовать к виду

Согласно сделанным ранее допущениям, минимальное время адсорбции и вероятность конденсаций постоянны для всех слоев, т. е. Toi=To2= … .т<и = =_. ..=То, a f, =f₂= … =ft= … =f. Тогда условие (2.20) с учетом уравнений (2.22) и (2.24) можно представить в виде системы уравнений:

где G— общее количество адсорбированного газа; А — полная поверхность адсорбента.

Обрабатывая экспериментальные данные G=f(p) в координа-

Р/Р_т             ,

тах ——— и р!рт, относительно которых записанное урав-

¹ — piP_T

некие линейно, можно найти две константы: А и С.

Константа С позволяет по известной теплоте конденсации рассчитать теплоту адсорбции.

Рассмотрим вывод уравнения (2.17). Условие адсорбционного равновесия для многослойной адсорбции (рис. 2.8) запишем в виде равенства скоростей конденсации в предыдущем адсорбционном слое и испарения в последующем слое:

Удельная скорость конденсации молекул в 1-слое

где fi — вероятность конденсации молекул в г-слое, У, — число молекул, ударяющихся в единицу времени о единицу поверхности. Воспользовавшись выражениями (1.14) и (1.18), перепишем (2.21) в виде

Удельная скорость испарения молекул

где а, — количество молекул, адсорбированных на единице поверхности; т_а, — время адсорбции молекул в i-слое.

С учетом выражения для времени адсорбции (2.3) уравнение (2.23) перепишем в виде                                                        <

Если учесть, что