Имитационное моделирование молекулярных потоков
Имитационное моделирование течения газа в вакуумных системах может осуществляться методом статистических испытаний (метод Монте-Карло). Это численный метод решения математических задач путем моделирования случайных величин с заданным законом распределения, построения вероятностных моделей и статистической оценки результатов. Этим методом можно решать любые задачи, сводя их к расчету математического ожидания. Наибольшее распространение метод статистических испытаний получил при решении как стационарных, так и нестационарных задач, связанных с течением газов в элементах вакуумных систем в высоком и среднем вакууме, когда движение каждой из молекул осуществляется хаотически путем последовательных столкновений со стенками элемента. Вероятность перехода молекул из одного сечения элемента вакуумной системы в другое определяется геометрией исследуемого элемента. По вероятностям перехода и известным концентрациям газа можно определить газовые потоки, возникающие в вакуумных системах.
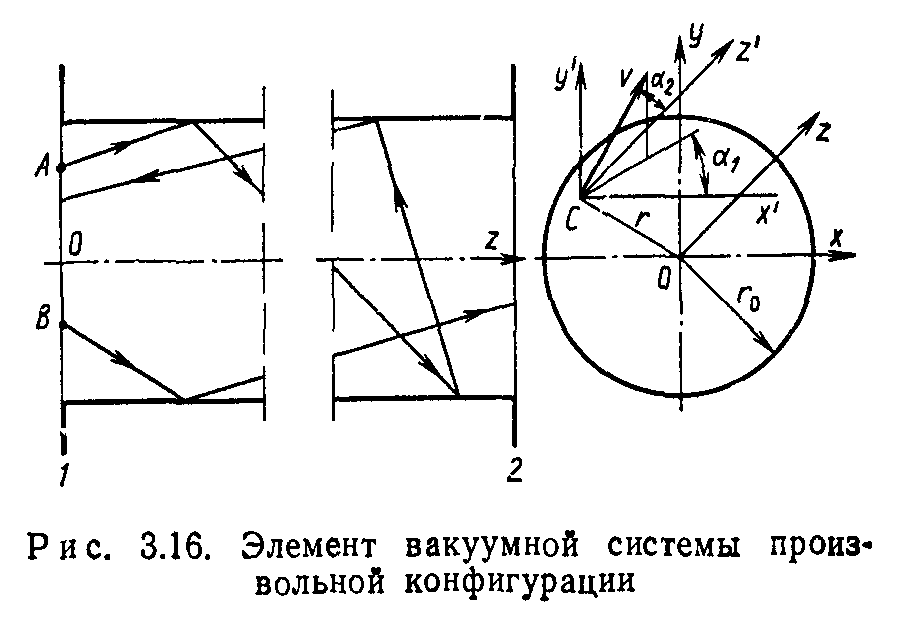
Рассмотрим применение метода статистических испытаний к моделированию стационарного течения газа через вакуумный элемент, имеющий один вход, один выход и произвольную внутреннюю конфигурацию (рис. 3.16). Исходными данными для расчета должны быть: конфигурация элементов, распределение молекул по площади входного отверстия, угловое распределение молекул на входе, угловое распределение молекул, десорбирующихся с внутренних поверхностей вакуумных элементов.
При удачном выборе положения системы координат уравнения (3.82) сильно упрощаются. Уравнение цилиндра, ось которого совпадает с осью z, имеет вид х2 + (/2 = г02; уравнение плоскости, перпендикулярной оси z, — вид ?=/ и т. д.
Условия на входе в элемент считаем соответствующими присоединению элемента к бесконечно большому объекту. Из молекулярно-кинетической теории известно, что из бесконечно большого объекта молекулы, попадающие во входное отверстие элемента, равномерно распределены по площади и имеют косинусное угловое распределение.
На стенках, ограничивающих внутреннее пространство элемента, принимаем, что десорбция молекул происходит в соответствии с законом косинуса.
Моделируемыми случайными величинами являются координаты точки входа молекулы в элемент и два угла, определяющие направление движения молекул в элементе от точки входа или с поверхности элемента.
Координатами точки входа для круглого входного отверстия (рис. 3.16) являются угол ф и радиус г. Для обеспечения равновероятного входа молекул по всей площади необходимо, чтобы угол ф был равномерно распределен в интервале от 0 до 2л. Генерируя датчиком случайных чисел, равномерно распределенным в интервале от 0 до 1, случайное число £ 0,1, получим случайную величину угла
Моделируя вероятность Р(г) новым случайным числом £ 0,1,
Конфигурацию элемента всегда можно с соотвествующими ограничениями приближенно описать набором уравнений второго порядка



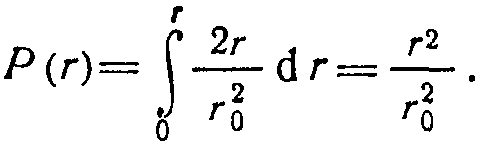
Вероятность попадания молекулы в круг площадью яг2
Для определения случайного радиуса входа молекулы в систему запишем число молекул, попадающих в кольцо шириной dr на радиусе г,
Уравнения (3.83) …(3.86) позволяют моделировать все необходимые для решения задачи случайные величины ср, г, си и а2.
В случае присутствия в элементе сорбирующих поверхностей должны быть заданы дополнительные случайные числа, характеризующие поглощение молекул.
Вероятностная модель стационарного течения газа описывает случайную траекторию движения молекул в элементе. Для математического моделирования траектории движущихся молекул газа воспользуемся уравнением прямой в локальной для каждой поверхности системе координат где Ь’, т’, п’ — направляющие косинусы каждой прямой в локальной системе координат, определяемые углами си и а2.
Для определения точки встречи молекулы с поверхностью элемента нужно преобразовать уравнение (3.87) в глобальную систему координат, в которой записаны уравнения, определяющие конфигурацию элемента: где хь уь Z — координаты точки вылета молекулы в глобальной системе координат; Ь, т, п — направляющие косинусы прямой в глобальной системе координат, которые определяют из преобразования
где blt bit Ь2 — направляющие косинусы глобальных осей по отношению к оси х’ mi, т2, т2— по отношению к оси у’-, rti, п2, Пз— по отношению к оси z’.
равномерно распределенным в интервале от 0 до 1, получим
Направление вектора скорости молекулы v в точке входа определяется двумя углами: си и а2 (рис. 3.16). Угол си образован осью х’ и проекцией вектора скорости на плоскость х’у’. Угол а2 образуется между осью г’ и вектором скорости п. В соответствии с принятыми граничными условиями случайный угол си равномерно распределен в интервале от 0 до 2л:
а для нахождения случайного угла а2, имеющего косинусное распределение, необходимо воспользоваться выражением (2.16):





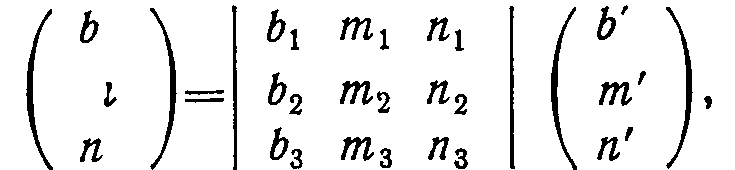
Совместное решение уравнения (3.88) со всеми уравнениями (3.82), определяющими конфигурацию элемента, позволяют получить точки пересечения. Пересечение прямой с плоскостью дает одну точку, с цилиндром — две. Логически могут быть отброшены точки пересечения, которые не лежат на внутренней поверхности элемента, в соответствии с ограничениями к уравнению (3.82) на внутренней поверхности элемента. Из оставшихся необходимо выбрать одну точку, находящуюся на минимальном расстоянии от исходной по направлению полета молекулы.
Для найденной таким образом точки пересечения вновь определяется случайное направление вылета. Углы вылета находятся аналогично си и а2 см. (3.85) и (3.86), при этом они измеряются в локальной системе координат, в которой ось z’ направлена по нормали к соответствующей поверхности вылета. Движение молекулы прослеживается до тех пор, пока она не покинет элемент через входное или выходное отверстие.
Исход каждого испытания есть случайная величина X, которая может иметь два значения: 0 и 1.
Будем считать, что молекула проходит элемент, когда Х=1. Траектория такой молекулы начинается от точки В на рис. 3.16.
Если молекула возвращается обратно, то Х = 0. Пример траектории такой молекулы, начинающейся от точки А, показан на рис. 3.16. Вероятность прохождения молекулой элемента от входного сечения 1 до выходного сечения 2 находится как среднеарифметическое значений случайной величины X при достаточно большом числе испытаний N: где Xi, …, XN— значения случайной величины X для соответствующего испытания.
Поток газа, проходящий через элемент, где Qo — поток газа, входящий в элемент через входное отверстие.
Проведем статистическую оценку результатов. Определим характеристики случайной величины X. Пусть М (X), М(Х2)’—математические ожидания случайных величин X и X2: где Pj — вероятности исходов Yi случайной величины X. Вероятность Р, соответствующая У1= 1, равна Pi-*2, а вероятность Р2, со-



где Р=1/(62у). При Pi~>2=0,5 необходимое число испытаний Л^=7?. В табл. 3.9 приведены значения числа испытаний 7? для различных значений относительной погрешности расчета 6 и вероятности выполнения оценки 1—у.
Из таблицы видно, что при Pi_>2=0,5 погрешность 10% с вероятностью 0,99 может быть достигнута при 10 000, а с вероятностью 0,9 — при 1000 испытаний.
Недостатком метода статистических испытаний является необходимость проведения большого числа испытаний для получения приемлемой точности, что требует применения вычислительной техники.
ответствующая Уг=0, равна 1—Pi->2- Таким образом,
Используем значения полученных математических ожиданий для нахождения дисперсии случайной величины X:
Среднеквадратичное отклонение случайной величины X
В соответствии с формулой Чебышева при любом фиксированном е>0
При достаточно большом числе испытаний N среднеарифметическое Хм отличается от М(Х) не более чем на е с вероятностью не менее чем 1—у, где
Относительная погрешность с учетом (3.95)
Воспользовавшись выражением (3.93) для D(X), преобразуем (3.96), тогда
При фиксированном значении у ошибка в расчетах убывает пропорционально корню квадратному из числа испытаний.
Число испытаний можно определить из (3.97):
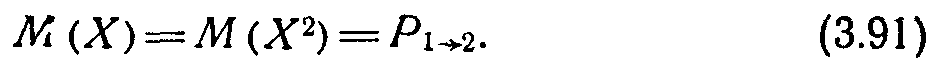

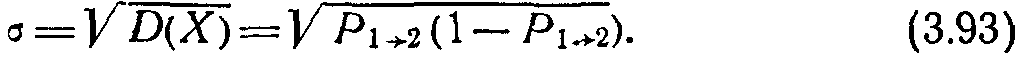





Значения коэффициента R
|
а |
1-? |
|||
|
0,99 |
0,98 |
0,97 |
0,96 |
|
|
0,01 |
1,0-106 |
5,0-105 |
3,3-10® |
2,5-105 |
|
0,02 |
2,5-105 |
1,3 105 |
8,3-104 |
6,3-104 |
|
0,03 |
1,1-105 |
5,6-104 |
3,7-104 |
2,8-104 |
|
0,04 |
6,3-104 |
3,1-104 |
2,1-Ю4 |
1,6-104 |
|
0,05 |
4,0-104 |
2,0-104 |
1,3-104 |
1,0-Ю4 |
|
0,10 |
1,0-Ю4 |
5,0-103 |
3,3-103 |
2,5-103 |
Продолжение табл. 3 9
|
а |
1-V |
|||
|
0,95 |
0,94 |
0,92 |
0,90 |
|
|
0,01 |
2,0-10s |
1,7-10® |
1,3-Ю5 |
1,0-Ю5 |
|
0,02 |
5,0-104 |
4,2-104 |
3,1-104 |
2,5-Ю4 |
|
0,03 |
2,2-104 |
1,9-104 |
1,4-Ю4 |
1,1-104 |
|
0,04 |
1,3-Ю4 |
1,0-104 |
7,8-103 |
6,3-Ю3 |
|
0,05 |
8,0-103 |
6,7-103 |
5,0-103 |
4,0-103 |
|
0,10 |
2,0-103 |
1,7-103 ’ |
1,3-Ю3 |
1,0-Ю3 |
Достоинством метода является универсальность вычислительного алгоритма. Для расчета нового элемента требуется только аналитически задать его конфигурацию.